AlphaGo用它下棋百度却用它解决更难的数学问题!
晓查 发自 凹非寺
量子位 报道 | 公众号 QbitAI
9102年,人类依然不断回想起围棋技艺被AlphaGo所碾压的恐怖。
却也有不以为然的声音:只会下棋的AI,再厉害也还是个运动员啊!
百度说:你们错了,它还是一位数学家。
百度硅谷AI实验室的同学们,就在用这个出自谷歌DeepMind的围棋算法,解决一个比围棋复杂得多的数学问题。
为了重新训练这个算法,百度用了300张1080Ti和2080Ti显卡。
他们解决的问题,叫做“图着色问题”,又叫着色问题,属于前些天让中国奥数队全军覆没的图论。它是最著名的NP-完全问题之一。
简单来说,就是用尽可能少的颜色,给一张图的顶点上色,保证相邻顶点的颜色不重复。
10个顶点的简单版是这样的:
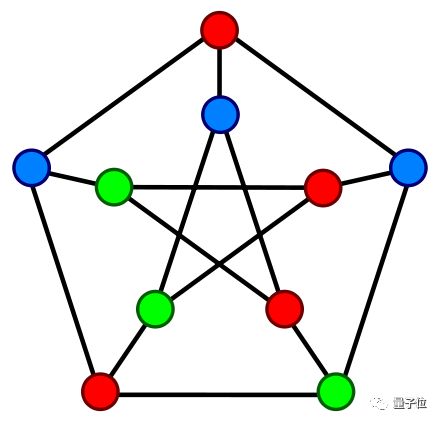
而复杂版……只要顶点足够多,分分钟让人类数学家无从下手,如果有512个顶点,这个问题的复杂度会比围棋高出几百个数量级。
在这个数学问题上,运动员AlphaGo表现优秀,最高能将一张图所用的颜色减少10%。
从四色定理谈起
就算你对“图论”、“着色问题”这些词有点陌生,应该也听说过“四色定理”。这是第一个由计算辅助证明的数学定理。
四色定理告诉我们,只需4种颜色我们就可以让地图上所有相邻国家的颜色互不相同。
这其实就是一个平面上的着色问题,国家可以简化为顶点,国与国之间的相邻关系可以简化为连接顶点之间的线。对于平面图而言,颜色数k最小等于几?
历史上数学家已经手工证明了五色定理(k=5),但是因为运算量太大,在将颜色数量进一步减少到四种(k=4)时却迟迟无法解决,最终在70年代靠计算机才完成证明。
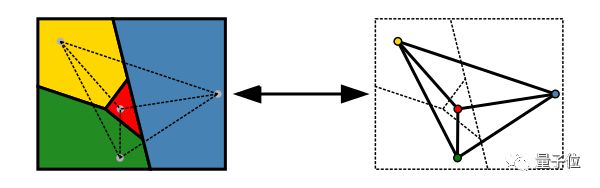
一般来说,我们可以用贪心算法解决这个问题,其基本思路是:先尝试用一种颜色给尽可能多的点上色,当上一步完成后,再用第二种尽可能多地给其他点上色,然后再加入第三种、第四种等等,直到把整张图填满。
或者是用深度优先搜索算法,先一步步给图像着色,若遇到相邻点颜色相同就回溯,再换一种着色方法,直到问题解决为止。
比围棋世界更复杂
如果图的顶点数比较少,以上两种方法还可行,但随着顶点数的增加,以上两种算法的局限性就暴露了出来。

△用贪心算法着色和最优解的对比
贪心算法会陷入局部最优解,而深度优先搜索算法的运算量会越来越大,以至于完全不可行。
图着色问题的复杂度随着顶点数增加而急剧增长。当顶点数达到512时,其可能得状态数就达到达到了10^790,远超围棋的10^460,当然更是比全宇宙的粒子数10^80多得多。

即使中等大小图的状态数也远超围棋,如果顶点数量达到1000万,复杂度会大得惊人,相当于在1后面有4583万个0。
另外着色问题还有另一个复杂维度,围棋算法可以反复在同一张相同棋盘上进行测试,而图即使顶点相同,因为连接各点的边不相同,结构也不完全相同。
从围棋中获得启发
这些更复杂的问题对算法的训练和推理提出了极大的挑战。而AlphaGo曾在解决这类复杂问题上取得了很大的成功,研究人员也很自然的想到了用它来解决图的着色问题。
对于这类问题,我们一般采用启发式搜索算法(heuristic search),就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到达到目标。
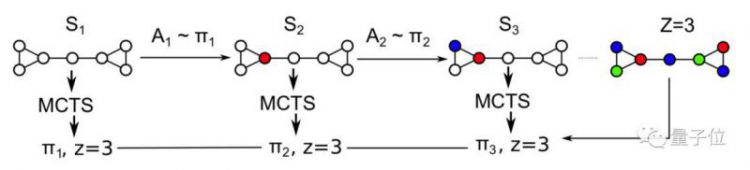
AlphaGo使用的蒙特卡洛树搜索(MCTS)用的就是一种启发式搜索算法。
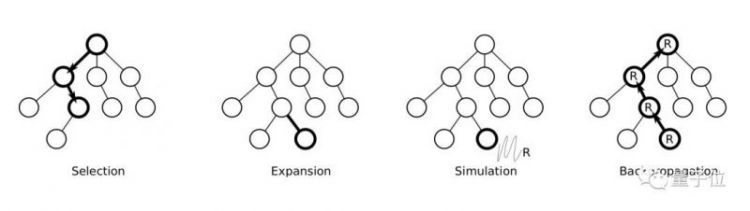
△蒙特卡洛树搜索算法示意图:选择路径;扩展树;由神经网络执行模拟;将最终结果反向传播,更新路径节点。
AlphaGo下棋通过正是这种方法,计算当前棋盘上获胜概率最大的点,直到赢棋为止。
图着色问题与围棋也有类似之处,它的每一步棋就是给接下来的点填上颜色。它和围棋和象棋一样都可以用强化学习来解决问题,差别则是奖励。
在图着色问题中,最明显的奖励选择是颜色种类,使用的种类越少越好。而在围棋和象棋中,奖励是游戏的胜负结果。
在棋类游戏中,让算法在自我对弈中进化是很一件很自然的事,让表现最好的学习算法与自己对抗,这就是AlphaGo的升级版本AlphaGo Zero。
AlphaGo Zero没有学习人类棋谱,它只是懂得围棋规则,在不断的对弈中获得提高,谷歌只用了21天,就让这个0基础的升级版打败了5-0战胜柯洁的AlphaGo Master版。
当AlphaGo进化到自学版本AlphaGo Zero后,它就更适合做图着色问题了,因为着色问题是没有所谓“人类棋谱”可以学习的。
在图着色问题种,研究人员让AlphaGo Zero与其他算法比赛,看谁用的颜色种类少,这就是算法的奖励机制。
原理
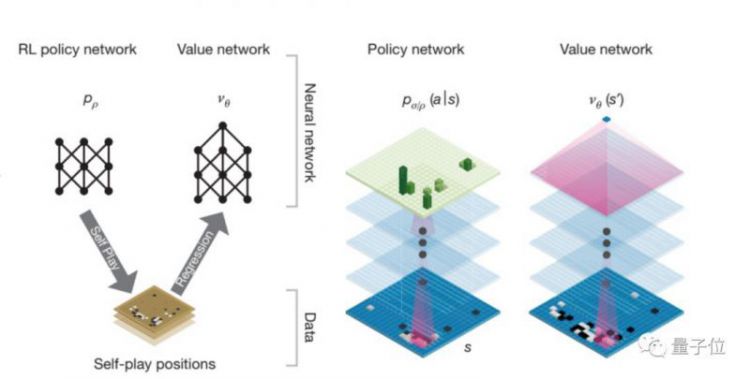
和AlphaGo一样,图着色算法也有策略网络(p-network)和价值网络(v-network),p是顶点涂某种颜色的概率,v是最终颜色数量少于之前最佳算法结果的概率。
而在围棋游戏中,p代表落子位置的概率,v代表最终获胜的概率。
为此,研究人员设计了一个快速着色网络(FastColorNet)。
对于这个网络,有如下要求:
1、可扩展性(Scalability):线性O(V)或线性对数O(E+VlogV)时间复杂度,保证它在更大的图形(比如1000万顶点)上也能使用。
2、完整图形上下文(Full Graph Context):不同的图有不同的着色策略,因此网络需要有图形结构的信息。
我们将该网络的损失定义为:
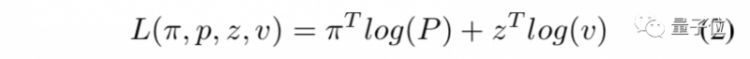
π代表当前行走步数,z代表当前使用的颜色数。

上图就是FastColorNet的架构。它的输入包含两个部分:问题上下文(problem context)和可能颜色上下文(possible color context)。
问题上下文(problem context)是根据刚刚着色的顶点,来安排接下来对哪些顶点进行着色。它在任务开始和结束的时候都是零。问题上下文中包含的顶点数是一个超参数,在实验中设置为8。
可能颜色上下文(possible color context)是以上顶点集合每种可能用到的颜色。它也是一个超参数,在实验中设置为4。
以上两个上下文都输入当策略网络和价值网络中。
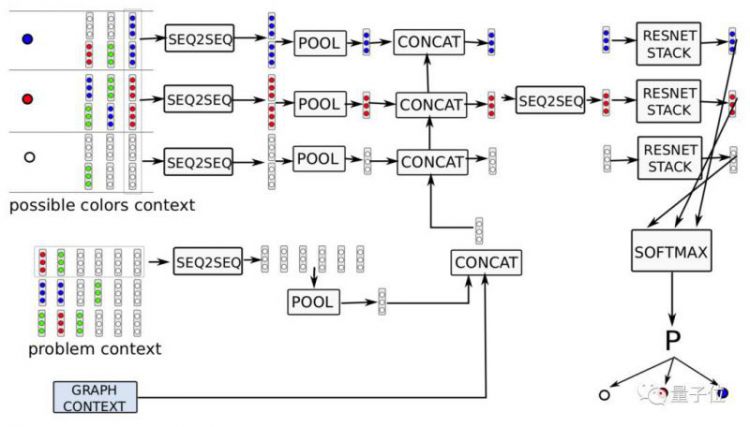
策略网络使用全局图形上下文(global graph context),它负责计算将每个颜色选择分配给当前顶点的概率。
随着填充过程的进行,颜色数量会逐渐增加。为了支持颜色数量的变化,它会首先独立处理每种颜色,产生一个非标准化分数,然后通过seq2seq模型对该分数进行处理,该模型还会考虑与其他颜色的依赖性。最终通过softmax操作得出归一化的填充颜色概率。
策略网络利用了具有相同颜色的节点之间的局部关系,提高了准确性,同时还降低了大图计算的时间复杂度。
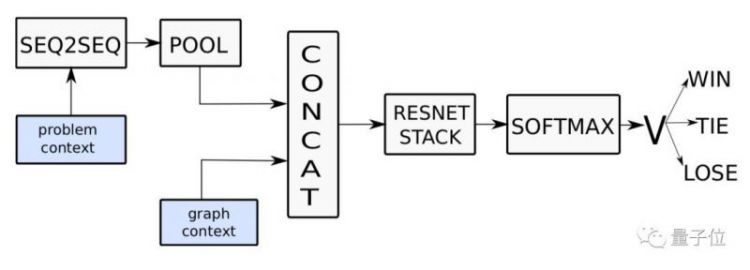
价值网络负责从输入数据预测着色问题最终的结果。 问题上下文(problem context)中的顶点与着色顺序存储在对应的序列中。使用seq2seq模型处理此序列,然后将这个序列与图形上下文(graph context)组合起来,并将它们馈送到完全连接的reLU层中,最终结果输入softmax,计算出胜利、失败或平局的概率。
结果
研究人员用FastColorNet的强化学习过程来训练图着色问题,图形大小从32个顶点到1000万个顶点不等。
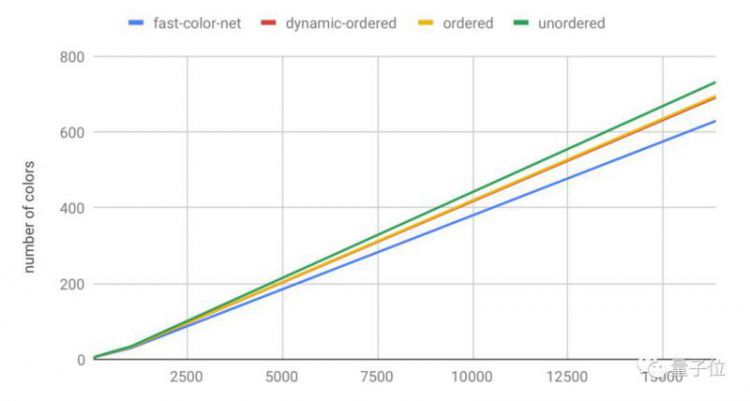
上图显示了图所需颜色的数量如何随顶点数量的增长而增长。

在32K到16M个顶点的图上进行测试,FastColor在训练集中使用的颜色比以往的启发式搜索算法提高了5%-10%。 尽管在测试集有所逊色,但性能也比先前的算法高出1%-2%。
虽然提升比例看起来不高,但这种算法显示出解决此类问题的潜力。Twitter上一位网友这样评价:这篇文章以线性复杂度O(n)解决了一个NP完全问题。

论文地址:
https://arxiv.org/abs/1902.10162
— 完—
相关文章
-
美国陆军成立『数字兵』计划,5.61亿美元用VR等新技术训练士兵
-
苏宁活成“别人家的公司”:逆势招聘、年终大赏、多维福利
-
啥年代了,还干重复工作呢?
-
留下一代人黑历史的大头贴相机,并没有被美颜app杀死
-
阿里AI入选全球十大突破性技术,它为何被比尔·盖茨看好?
-
深度资讯|格力、奥克斯公开battle,抢占线上零售增长点
-
全球零售业最高奖项为何颁给阿里?
-
中国移动互联网:正在消失的红利和即将衰退的巨头
-
爱奇艺Q1财报解读:营收超预期会员单季增长1200万
-
也谈张小龙和张一鸣:产品经理的时代结束了?
-
【虎嗅晚报】《流浪地球》将延长上映2个月;阿里大文娱回应:分工去年宣布,不是新闻
-
计算机信息系统集成资质是否取消?
-
产品升级|集团连锁整合招生上线
-
禁毒知识抢答模拟系统、机器人禁毒宣传、智能化禁毒机器人
-
深度资讯 | 中国智能手机要把工厂开满印度,增量市场可能进入最后一战
-
安卓手机备忘录在什么地方打开
-
兄弟打印机怎么连接电脑打印文件
-
从SARS到新型肺炎,17年后的互联网改变了什么?
-
AI在爱奇艺商业广告中的应用和探索
-
深度资讯|PayPal曲线入华,与支付宝微信角力跨境电商
-
麻花影视在两平台被下架!盗版《流浪地球》播放数百万,拒不删除
-
市场费用居高不下,供应链优化难上牌桌,明星公司拼多多的发展难题
-
一文了解云计算,全世界一台计算机
-
苹果7防水到什么程度
-
可惜发得有点迟!6英寸+高通632+1200万双摄,魅族Note8买不买
-
【钛晨报】团王兴回应不支持支付宝:淘宝为什么不支持微信支付;中通快递收购海尔旗下日日顺乐家快递柜
-
技术变聪明会场更智慧
-
金立:《复盘金立死亡之谜》一文捏造事实 严重侵害公司声誉
-
雷军:小米下一个目标,三年做到全球第一